Fitting transport laws

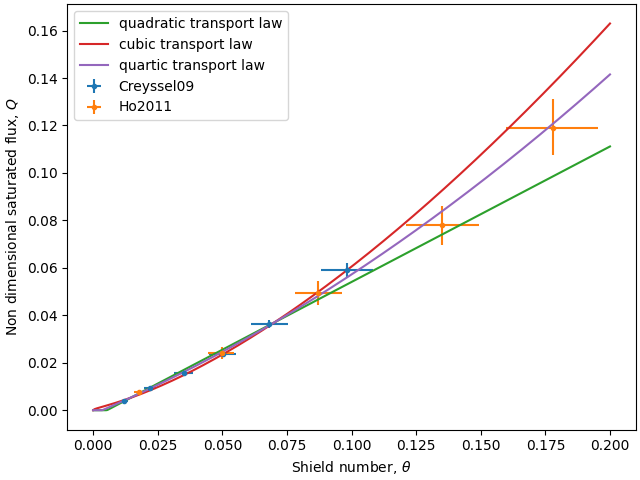
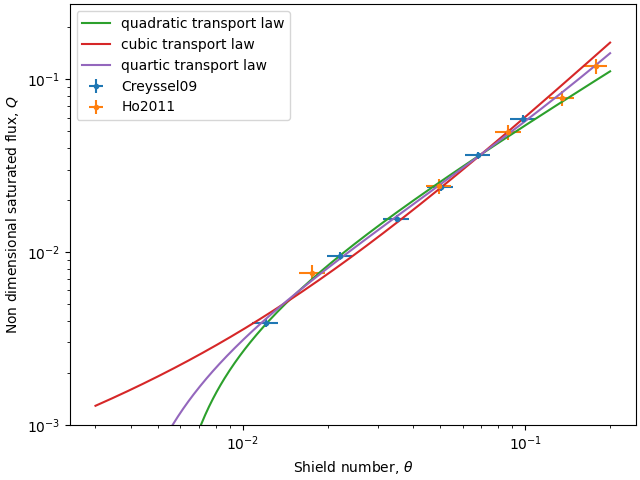
Fitting the different transport laws to the laboratory data of:

- [1] Creyssels, M., Dupont, P., El Moctar, A. O., Valance, A., Cantat, I., Jenkins, J. T., … & Rasmussen, K. R. (2009). Saltating particles in a turbulent boundary layer: experiment and theory. Journal of Fluid Mechanics, 625, 47-74.

- [2] Ho, T. D., Valance, A., Dupont, P., & El Moctar, A. O. (2011). Scaling laws in aeolian sand transport. Physical Review Letters, 106(9), 094501.

• 
• 

quadratic transport law: $\omega = 7.81$, $\theta_{\rm th}$ = 5.34e-03
cubic transport law: $\omega = 1.73$, $\theta_{\rm th}$ = -1.06e-02
quartic transport law: $\theta_{\rm th}$ = 3.52e-03

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from pydune.physics import (quadratic_transport_law, cubic_transport_law, quartic_transport_law)

# Loading the different data
Data_creyssel09 = np.load('../src/Data_creyssel09.npy',
                          allow_pickle=True).item()
Data_Ho2011 = np.load('../src/Data_Ho2011.npy',
                      allow_pickle=True).item()
Datasets = {'Creyssel09': Data_creyssel09, 'Ho2011': Data_Ho2011}

# preparing data for fits
shield = np.concatenate([Datasets[dataset]['Shield'] for dataset in sorted(Datasets.keys())])
shield_err = np.concatenate([np.abs(Datasets[dataset]['Shield'] - Datasets[dataset]['Shield_err']).mean(axis=0)
                             for dataset in sorted(Datasets.keys())])
Q = np.concatenate([Datasets[dataset]['Q_adi'] for dataset in sorted(Datasets.keys())])
Q_err = np.concatenate([np.abs(Datasets[dataset]['Q_adi'] - Datasets[dataset]['Q_adi_err']).mean(axis=0)
                        for dataset in sorted(Datasets.keys())])

# ### transport laws used
laws = [quadratic_transport_law, cubic_transport_law, quartic_transport_law]
labels = ['quadratic transport law', 'cubic transport law', 'quartic transport law']
p0_s = [[0.01, 6], [0.02, 4], [0.02]]  # initial guesses to help fit convergence

theta_plot_lin = np.linspace(0, 0.2, 400)
theta_plot_log = np.logspace(np.log10(3e-3), np.log10(2e-1), 400)

for i, theta_plot in enumerate([theta_plot_lin, theta_plot_log]):
    fig, ax = plt.subplots(1, 1, constrained_layout=True)
    # #### plotting datasets
    for dataset in Datasets.keys():
        ax.errorbar(Datasets[dataset]['Shield'], Datasets[dataset]['Q_adi'],
                    xerr=np.abs(Datasets[dataset]['Shield'] - Datasets[dataset]['Shield_err']),
                    yerr=np.abs(Datasets[dataset]['Q_adi'] - Datasets[dataset]['Q_adi_err']),
                    linestyle='None', label=dataset, fmt='.')
    # ### fitting and ploting results
    for law, label, p0 in zip(laws, labels, p0_s):
        p, pcov = curve_fit(law, shield, Q, sigma=Q_err, absolute_sigma=True, p0=p0)
        ax.plot(theta_plot, law(theta_plot, *p), label=label)
        #
        if i == 1:
            if p.size == 2:
                print(
                    r"""{}: $\omega = {:.2f}$, $\theta_{{\rm th}}$ = {:.2e}""".format(label, p[1], p[0])
                )
            else:
                print(
                    r"""{}: $\theta_{{\rm th}}$ = {:.2e}""".format(label, p[0])
                )

    ax.set_xlabel(r'Shield number, $\theta$')
    ax.set_ylabel('Non dimensional saturated flux, $Q$')
    ax.legend()
    if i == 1:
        ax.set_xscale('log')
        ax.set_yscale('log')
        ax.set_ylim(bottom=1e-3)
    plt.show()